猫も杓子も構造化

発達障害、特別支援などについて書いています。最近は心理学関係の内容が多めです。

日本版WISC-Vは今

調べたこと・考えたこと

ブログへのアクセスを見ると、WISC-Vの動向が気になる人が多いようで、英語で書かれた資料をまとめた次のページへのアクセスが多い。

nekomosyakushimo.hatenablog.com


日本語版の開発状況がどうなっているのかというと日本文化科学社のサイトに次のようなページが出来ていた。

日本版WISC-V知能検査 予備調査・実施協力者募集要項｜日本文化科学社

ページによれば、新しい検査内容のパイロット調査が終わり全国規模の予備調査がこの10月から開始されるそうだ。予備調査ということで、その結果を踏まえてその後の本調査に続いていくのだろうから、出版はまだ先のことになるでしょうか。進捗が気になる方は日本文化科学社のサイトをちょくちょくチェックしてみても良いのかもしれない。

LD学会所感

調べたこと・考えたこと

10月7日から9日の間に宇都宮で開催されたLD学会に参加してきた。きれいなまとめや読者に有益なまとめなどは目指さず（というか私には出来ませんし）、拡散した思考を書き散らかしておく。

親の会のシンポ、ローラクリンガー先生による特別公演、内山先生による教育講演など自分が参加したプログラムでは成人生活と教育の接点を考える機会が多かった。ローラ先生の講演では、”professional social skills”という言葉が印象に残っている。通訳の方はたしか「職業人としてのソーシャルスキル」みたいな訳し方をしていたと思う。日本の学校教育の文脈でソーシャルスキルが言及されるときは、「友達を作る」とか「相手の気持ちを考える」とかフレンドシップに関わるソーシャルスキルが想像されがちだが、ローラ先生の言うところによると職業人としてのソーシャルスキルは、困った時に支援を要求するなど職業生活で必要とされるソーシャルスキルのことを指すらしい。IQが高いASDの人でも、いつ、だれに、何を聞けば良いか分からず机の前で困ったままでいることが多い例などを挙げていた。同様な話は内山先生の講演や親の会シンポの中でも触れられていた。

ASDの人のフレンドシップに関連して、内山先生が講演の中で「少数の人との淡くて良好な関係を目指す」とのようなことをおっしゃっていたことも印象に残っている。この「淡くて」という部分がとても大切で、それが抜け落ちてしまうと、定型発達と同じような対人関係を目指すか、対人関係なんて一切いらない、の極端なものしか選択肢がなくなってしまい、ASDの人にとってはどちらもとてもしんどい選択肢になってしまうだろう。インタビューの中でASDの人も孤立・孤独は嫌だという話があり、「丁度良い」「心地いい」人間関係の構築を個別化された支援の中で見出していくことの必要性を感じた。

LD学会は学校の先生の参加者が多い。その関係もあってか参加したプログラムでは、成人生活で必要なことの議論に続き、それらをいかに学校教育の中で準備していくかというような話の流れが多かった。将来必要なことから逆算的に教育内容を検討するというのはとても重要なことに思うし、とりわけ成人生活との接続を検討する際には欠かせない視点だろう。ただ、それと同時に将来必要なことを前もって準備することには限界というものがあるだろうことも感じる。どういうスキルが必要になるかは、その人が置かれる成人生活の環境にもよるだろうから個別化・具体化が必要になる。しかし、個別化・具体化を学校教育の早期から行うことは現実には難しい側面もあるように思う（将来どんな進路になるかが小学1年生で決まっている例はまれでしょう）。となると必然的に、どんな進路になろうがある程度有益なスキル（例えば、日常生活的なものや生活習慣的なものとか）になるか、抽象的な目標（コミュニケーション能力（笑）や社会人基礎力（笑）のような）になりがちな気がする。

これは前々から言っていることなのだが、「前もって準備する」だけでなく、「必要になった時に必要な支援が受けられる」ということがあれば良いのにと思っている。学校教育の関係者はとかく「何かを教えて子供が変わる」ことにロマンを持っている人が多いのか、教育して子供を変えることが子供の幸せを達成するための最初の（そして唯一の）選択肢になりやすいように思う（それが仕事だから仕方ないけど）。でも、教育ってそんなパワフルなものじゃなくて、それこそ変えられないことの方が多いんじゃないの、って私はややネガティブに教育を考えている（だから、何もしなくて良いという話でなくて、変えられることに資源を重点的に分配しましょうという話。）。全部を教育の「中」でやりくりするのでなく、必要になった時に必要な支援が受けられるようになったり、一度失敗をしてもサポートを受けながら再挑戦できるような仕組みがあったりする社会の方がずっと素敵なものなのじゃないかと思う。支援というものを学校教育という学校を中心とした枠組みから考えるのでなく、社会の中で生活を営む本人を中心した枠組みで捉え、必要なサポートが「だれ」によって「いつ」「どこで」受けられるのかを整理して、サポートの適切・適当な分担を考えいくことが今後より必要となってくるのではないかと感じた。

他にも、考えたことは色々とあるけれどもとりあえず今日はここまで。


【やや関連すること】
nekomosyakushimo.hatenablog.com

必要なサンプルサイズの大きさは（実験編）

調べたこと・考えたこと

前回の記事で、調査を行い母集団における比率を求める際に、誤差を任意の範囲内に収めるための計算について書いた。比率については、

　　 \displaystyle n = \left( \frac{1.96}{E} \right)^2 p(1-p)

の式の、Eの部分に収めたい範囲の誤差を代入すると求まることが分かった。

式の上では理論的に求まったものの本当にこれで誤差が所定の範囲内に収まるのか試してみたくなるのが世の常である。ということで、毎度おなじみRを用いたシミュレーションである。

前回の記事で、95%水準で誤差を5%、3%、1%に収めたいときに必要なサンプルサイズは、上の式をそれぞれについて解いて385、1068、9604だと書いた。本当にこの通りになっているか確認してみよう。

まず、二項分布で乱数を発生させる。二項分布の乱数発生の関数はrbinom(n, size, p)である。引数には順番に「観察の回数」「試行の回数」「試行における成功確率」を指定する。今やりたいことに当てはめて考えると、nにはシミュレーションの回数を、sizeにはサンプルサイズを、pには母集団における確率を指定する。シミュレーションの回数はまぁ大体10000回もやればとりあえず良いでしょう。pには計算に用いた0.5を指定しておく。

dat <- rbinom(10000,385,0.5)
head(dat)
# [1] 207 190 198 193 203 185 
length(dat)
# [1] 10000

head関数で中身を除いた結果から分かるように、成功率0.5で385回の試行における成功数についてのデータがそれぞれ発生する。データの個数は当然10000である。

このままだと、比率のデータではないが、サンプルサイズで割るとこれが比率になる。で、ここで得られた標本比率が母集団の比率である50%より5%以上ずれているかを調べたい訳なので、45%より小さいあるいは55%より大きい標本比率の数を数えることにする。その数をシミュレーションの回数で割れば一体何%ぐらいが5%よりも大きな誤差であったかが分かるはずである。

dat <- dat/385
over <- length(dat[dat > 0.55]) + length(dat[dat < 0.45])
over/10000
# [1] 0.0509

結果を見ると分かるように、標本比率の内5%ほどのデータが5%より大きい誤差であることが分かる。逆に言えば、信頼係数である95%の標本は誤差5%以内に収まっているということである。

発生させた比率のデータのヒストグラムは以下のようになる。

f:id:nekomosyakushimo:20171001122622p:plain

正規分布っぽい形をしたこのヒストグラムの両裾が全体の内の5%になる点が、0.45と0.55であるということになろう。

誤差の水準およびサンプルサイズを変えて同様の実験を繰り返し、ヒストグラムを出力したものが次のもの。

f:id:nekomosyakushimo:20171001123034p:plain

f:id:nekomosyakushimo:20171001123045p:plain

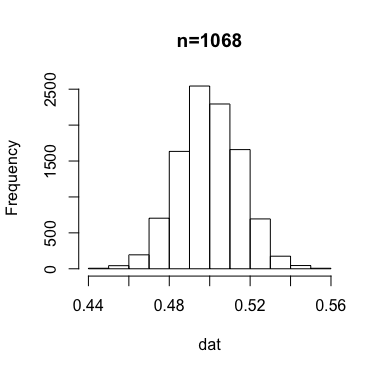
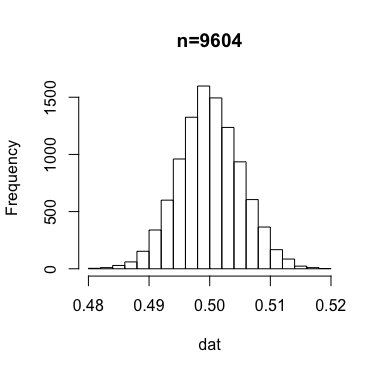
x軸の値に注目していただければ分かるが、サンプルサイズが大きくなるほど、誤差が小さくなっていくのが分かる。それぞれ何パーセントぐらいの結果が、指定した誤差の水準を上回っているかを確認すると、

dat <- rbinom(10000,1068,0.5)
dat <- dat/1068
over <- length(dat[dat > 0.53]) + length(dat[dat < 0.47])
over/10000
# [1] 0.0474

dat <- rbinom(10000,9604,0.5)
dat <- dat/9604
over <- length(dat[dat > 0.51]) + length(dat[dat < 0.49])
over/10000
# [1] 0.0515

やはり5%ぐらいが指定した誤差の水準をオーバーしている。そういう風に値を設定したのだから当然と言えば当然だろうか。微妙に5%とはずれているが、シミュレーションの数を限りなく大きくしていけばこの値は5%に限りなく近づいていくだろう（正確には5%より少しだけ小さい値。サンプルサイズの計算のとき小数点以下を切り上げたから）。

そういえばサンプルサイズの決め方に焦点を当てた本というのがいくつか出ていて、読もう読もうと思って放置していたのだけれど今度どれかを読んでみようかしら。

心理学のためのサンプルサイズ設計入門 (KS専門書)

心理学のためのサンプルサイズ設計入門 (KS専門書)

サンプルサイズの決め方 (統計ライブラリー)

サンプルサイズの決め方 (統計ライブラリー)

サンプルサイズの設計 (臨床家のための臨床研究デザイン塾テキスト)

サンプルサイズの設計 (臨床家のための臨床研究デザイン塾テキスト)

必要なサンプルサイズの大きさは

調べたこと・考えたこと

先日社会調査に関連した話の中で、「完全に無作為抽出が達成されてたとしたらサンプルサイズがどれくらい必要か」についての話になった。「今の首相を支持するかどうか」のようなシンプルな比率の調査をする際にどれくらいのサンプルの大きさがあれば信頼に足るのかを例に考えてみる。

仮に、現在の首相の支持率が母集団において0.3だとする。で、この母集団からn人だけ標本抽出をするのだが、それぞれの人の回答というのが独立していると考えると、これは B(n, 0.3)の二項分布に従うことになる。

二項分布の期待値は E(x) = npであるため、この場合の期待値は E(x) = 0.3nである。10人から回答を得るとすると、支持者は平均的に3人になるし、100人から回答を得るとすると、支持者の数は平均的に30人になる。（平均的にというのは、同じnで標本抽出を繰り返せば28人とか33人とか数値を得ることもあるけど、それらの標本値の分布の平均は30人になるということ。）

続いて二項分布の分散は V(x) = np(1-p)なので、この場合は V(x) = 0.21nになる。そして、その標準偏差は \sigma (x) = \sqrt{0.21n}になる。例えば、100人から回答を得たのであれば \sigma (x) = \sqrt{21} = 4.582 となる。

さて今、関心があるのは支持率という比率であるので実現値をnで割ると、

\displaystyle E\left(\frac{x}{n} \right) = \frac{1}{n}E(x) = p

となり期待値はpになる。

分散と標準偏差はどうなるかというと V(ax) = a^2 V(x)であるから、

\displaystyle V(\frac{x}{n}) = \frac{1}{n^2}V(x) = \frac{np(1-p)}{n^2} = \frac{p(1-p)}{n}

\displaystyle \sigma(\frac{x}{n}) = \sqrt{\frac{p(1-p)}{n}}

となる。

ところで、二項分布はnの数が十分に大きければ正規分布で近似ができるのであった。すなわち、標本から得られた比率 x/nは、近似的に N(p, p(1-p)/n)に従う（今求めた期待値と分散）。そこで、信頼係数95%で、

\displaystyle \frac{\left| \frac{x}{n} - p \right|}{\sqrt{\frac{p(1-p)}{n}}} < 1.96

である。ここで、推定の誤差を | x/n - p |を一定の値E以内にしようとしたときに、 | x/n - p | = Eと置いて上の式に代入し、不等号を=にしてnについて解くと、

\displaystyle \frac{E}{\sqrt{\frac{p(1-p)}{n}}} = 1.96

\displaystyle \frac{E}{1.96} = \sqrt{\frac{p(1-p)}{n}}

\displaystyle \left(\frac{E}{1.96}\right)^2 = \frac{p(1-p)}{n}

\displaystyle n = \frac{p(1-p)}{(\frac{E}{1.96})^2}

\displaystyle n = \left( \frac{1.96}{E} \right)^2 p(1-p)

が得られる。このEに任意の値を入れることで、確率95%で誤差がEに収まるためのnを求めることができる。

ただ、計算のためにはpの値が必要なのだが、調査を行う前にはこのpが分からないのが普通である（分かっていたのならばそもそも調査などしない！）。 p(1-p)の取りうる最大値は0.25であるので、とりあえず p=0.5にして計算をすれば大きめに標本サイズを見積もることになるが安全だろう。

最初の例にもどり支持率を調査しようと思った場合に、誤差3%に押さえたいとする。Eに0.03を代入すると

\displaystyle n = \left( \frac{1.96}{0.03} \right)^2 0.5(1-0.5) \simeq 1067.1

が得られる。すなわち、サンプルサイズを1068以上にすれば、95%の確率で標本から得られた支持率が、母集団における支持率と3%以上離れていないと考えることができる。

ちなみに誤差を5%以内にすると必要なサンプルサイズは385、誤差を1%以内に抑えようとすると9604必要になる。1%単位の誤差で必要なサンプルサイズは結構変わるものである。

ちなみにちなみに、大まかな支持率に当たりが付いているのであれば計算式の p(1-p)のとる値は小さくなるので必要な標本サイズも小さくなる。

【参考】
宮川公男　基本統計学（有斐閣）

基本統計学 第4版

基本統計学 第4版

バイスプライヤーすごい（セローのエンジンオイル交換に伴うアレコレ）

その他

セローのエンジンオイルを交換したのですが、そのとき想定外に手間取ったことに関するメモ。

手順は下記のサイトを参考にしました。

セロー250メンテナンス オイル交換方法 | セロー250でバイク旅

ただオイルを抜いて入れるだけの話なので難しいこともないはずなのですが、ドレンボルトをソケットレンチで回そうと力を入れるも全然回らず。さらに力を入れるとぐにゃっと嫌な感触とともにレンチが回り、ボルトの頭をなめてしまっています。

そこからは、ボルトを回そうと力を入れるとボルトをなめる一方で、一向にボルトは緩まず。

グーグル先生に聞いたところによれば、似たような事態に陥っているケースはままあるようです。

なめてしまった ボルトのはずし方 教えてください。 - バイクの... - Yahoo!知恵袋
ルート5 : なめったボルトとナットツイスター
WR250Xのオイル交換！純正ドレンボルトはナメりやすいので初心者は注意！ | WR250Xで進行形！

で、手持ちの工具だとどうにもならなそうだったので、上記の体験談を参考に一番安く済みそうなバイスプライヤーを近くのホームセンターで購入して、なんとかすることに。

バイスプライヤーってのは、ロッキングプライヤーとも言われたりすることもある、

トップ(TOP) バイスプライヤ VP-125

トップ(TOP) バイスプライヤ VP-125

こんな工具のことで、挟んだものをかなり強固に固定できるものだそうです。ホームセンターのプライベートブランドの安物で700円程度でした。

あと、ドレンボルトは交換が必要なので、ネットで評判が良さそうだった

キジマ(Kijima) ワイヤーロックドレンボルト 105-112

キジマ(Kijima) ワイヤーロックドレンボルト 105-112

これを注文しました。ボルトの頭が純正よりかはかなり大きいので今後なめる心配もなさそうです。（ワイヤーでロックもできるそうですが、私はレースに出るとかとは関係ないのでワイヤーはつけていません。）

で、バイスプライヤーでがっちりとボルトを固定して力を加えると、思ったよりあっさりと回ってくれて無事になめてしまったドレンボルトをはずすことに成功。その後は特に困ることもなくいつも通りの手順で交換できました。

問題となっていたドレンボルト。

f:id:nekomosyakushimo:20170927160910j:plain

六角形の角がつぶれて丸みを帯びてきています（レンチで力づくで何度か回したから）。ギザギザしているのはバイスプライヤーが食い込んだ部分です。がっちりと噛んで固定したことが分かります。

二項分布の4次のモーメントの導出

調べたこと・考えたこと

前回までで3次のモーメントをやったんだから次は4次だろう（安易）。

nekomosyakushimo.hatenablog.com
nekomosyakushimo.hatenablog.com

原点まわりのモーメントの導出

まず、モーメント母関数を3回微分したのものがこちら。

　　 \begin{split} f^{\prime\prime\prime}(\xi) &= np \{ (n-1) 2pe^{2\xi}(pe^\xi + q)^{n-2} + (n-1)(n-2)p^2e^{3\xi}(pe^\xi +q)^{n-3}\\ \\ &\quad + e^\xi (pe^\xi + q)^{n-1} + (n-1)pe^{2\xi} (pe^\xi + q)^{n-2} \} \end{split}


これを、（大変に面倒くさいけど）さらにもう1回微分すると、

　　 \begin{split} f^{\prime\prime\prime\prime}(\xi) &= np \{ 4(n-1)pe^{2\xi} (pe^\xi + q)^{n-2} + 2(n-1)(n-2)p^2e^{3\xi}(pe^\xi +q)^{n-3}\\ \\ &\quad + 3(n-1)(n-2)p^2 e^{3\xi}(pe^\xi + q)^{n-3} + (n-1)(n-2)(n-3) p^3e^{4\xi} (pe^\xi + q)^{n-4} \\ \\ &\quad + e^\xi(pe^\xi + q)^{n-1} + (n-1) pe^{2\xi}(pe^\xi + q)^{n-2} \\ \\ &\quad + 2(n-1) pe^{2\xi}(pe^\xi + q)^{n-2} + (n-1)(n-2) p^2e^{3\xi}(pe^\xi + q)^{n-3} \} \end{split}


このような形になる。次に、 \xi =0とおき、次数を揃えながら整理していくと、

　　 \begin{split} f^{\prime\prime\prime\prime}(0) &= np \{ 4(n-1)p + 2(n-1)(n-2)p^2 + 3(n-1)(n-2)p^2 + (n-1)(n-2)(n-3) p^3 \\ \\ &\quad + 1 + (n-1) p + 2(n-1) p + (n-1)(n-2) p^2 \}\\ \\ &= np \{ (n-1)(n-2)(n-3) p^3 + [(n-1)(n-2) + 2(n-1)(n-2) + 3(n-1)(n-2) ] p^2 \\ \\ &\quad + [ 4(n-1) + 2(n-1) + (n-1)]p + 1 \}\\ \\ &= np \{ (n-1)(n-2)(n-3) p^3 + 6(n-1)(n-2)p^2 + 7(n-1)p + 1 \} \\ \\ &= n(n-1)(n-2)(n-3) p^3 + 6n(n-1)(n-2)p^3 + 7n(n-1)p^2 + np \end{split}

が求まる。これが二項分布の4次の原点まわりのモーメントである。

平均値まわりのモーメントの導出

次に、平均値まわりでのモーメントを求めてみよう。求める値は、

　　 \displaystyle \begin{split} m_4 &= E\big( (x - \mu)^4 \big) = E(x^4 -4x^3 \mu + 6x^2\mu^2 -4x\mu^3 + \mu^4 )\\ \\ &= E(x^4) -4\mu E(x^3) + 6\mu^2 E(x^2) -4\mu^3 E(x) + \mu^4 \\ \\ &= E(x^4) -4\mu E(x^3) + 6\mu^2 E(x^2) -3\mu^4 \end{split}


である。各項に原点まわりのモーメントを代入すると、

　　 \begin{split} m_4 &= n(n-1)(n-2)(n-3)p^4 + 6n(n-1)(n-2)p^3 + 7n(n-1)(n-2)p^2 + np \\ \\ & \quad - 4np\{n(n-1)(n-2)p^3 + 3n(n-1)p^2 + np\} + 6n^2p^2 \{n(n-1) + np\} -3n^4p^4 \end{split}


となる。とりあえず強引に全部展開すると、

　　 \begin{split} m_4 &= n(n-1)(n-2)(n-3)p^4 + 6n(n-1)(n-2)p^3 + 7n(n-1)(n-2)p^2 + np \\ \\ & \quad - 4n^2(n-1)(n-2)p^4 -12n^2(n-1)p^3 -4n^2p^2 + 6n^3(n-1)p^4 +6 n^3p^3 -3n^4p^4 \end{split}


になり、それを pの次数で整理すると、

　　 \begin{split} m_4 &= (3n^2 -6n)p^4 + (-6n^2 +12n)p^3 + (3n^2 -7n)p^2 + np \end{split}


が得られる。3次までの平均まわりのモーメントでは、 npおよび (1-p)が登場していたことに注意をしつつ、これを因数分解していくと、

　　 \begin{split} m_4 &= (3n^2 -6n)p^4 + (-6n^2 +12n)p^3 + (3n^2 -7n)p^2 + np \\ \\ &= 3n^2p^4 - 6np^4 -6n^2p^3 + 12np^3 + 3n^2p^2 - 7np^2 + np \\ \\ &=np\{ 3np^3 - 6p^3 -6np^2 + 12p^2 + 3np - 7p + 1 \}\\ \\ &=np\{ 3np^3 - 6np^2 + 3np - 6p^3 + 12p^2 - 6p + 1 - p \}\\ \\ &=np\{ 3np(p^2 - 2p + 1) -6p (p^2 -2p + 1) + 1 - p \}\\ \\ &=np\{ 3np(1 - p)^2 -6p (1 - p)^2 + 1 - p \} \\ \\ &=np\{ (3np -6p)(1 - p)^2 + 1 - p \} \\ \\ &=np(1-p)\{(3np -6p)(1 - p) + 1 \} \\ \\ &=np(1-p)\{1+ 3(n - 2)p(1 - p)\} \end{split}


が求まる。これが、平均まわりの4次のモーメントである。非常に煩雑な計算であった。

続・二項分布の3次のモーメント

調べたこと・考えたこと

前回の記事で、モーメント母関数を用いた二項分布の3次のモーメントの導出について書いた。今回は、二項分布から抽出したデータの分布を実際に見ながら3次のモーメントと分布の形にについてみてみる。

Rのデフォルトの関数には、歪度を計算するものはないらしい。momentsというパッケージを入れれば、その中にskewness()という歪度を計算する関数があるので今回はそれを使う。

まずは、成功確率 pが異なる二項分布から、それぞれ n = 1000程度でデータを発生させる。

dat1 <- rbinom(1000,10,prob=0.5 )
dat2 <- rbinom(1000,10,prob=0.25)
dat3 <- rbinom(1000,10,prob=0.75)
dat4 <- rbinom(1000,10,prob=0.10)
dat5 <- rbinom(1000,10,prob=0.90)

それぞれのデータで歪度を求めるとともに、度数分布をプロットしてみる。

まずは、 p= 0.5のものから。

f:id:nekomosyakushimo:20170915225523p:plain

a_3 = -0.0515で、0に近い。分布もそれに対応して概ね左右対称である。

続いて、 p= 0.25のものを見る。

f:id:nekomosyakushimo:20170915225731p:plain

a_3 = 0.373である。歪度は正の値だと、右の裾が長くなると言われており、分布からも確認することができる。

今度は、 p = 0.75。

f:id:nekomosyakushimo:20170915230344p:plain

a_3 = -0.382であり、負の値なので左の裾が長くなっている。一つ前のものと比べると絶対値は似たような値であり、分布の歪みの程度が大体同じであることを示している。

より偏りのある p= 0.10で見てみよう。

f:id:nekomosyakushimo:20170915230750p:plain

a_3 = 0.991であり、より大きな偏りを持ち、右の裾の長い分布であることが分かる。

最後は p= 0.90。

f:id:nekomosyakushimo:20170915231059p:plain

a_3 = - 0.899で、予想通りに左に裾が長い分布が確認できる。

歪度を求めると分布の形についてより詳細に分かるので、分布の形状を確かめるときには算出すると良いでしょう。