相関係数の標本分布について - 猫も杓子も構造化

はじめに

『心理統計学の基礎』のp.114に相関係数の標本分布が図示されている。確率密度関数は数学的にかなり複雑だからとの理由で省略される代わりに近似的にその期待値を求める式が載っている。

$\displaystyle{ \mu_r = \rho - \frac{ \rho (1- \rho^2)}{2N} }$

その標本誤差についてもやはり近似的に求める次のような式が載っている。

$\displaystyle{ \sigma_r = \frac{ 1- \rho^2}{\sqrt{N}} }$

これらの近似的なものでもさして困らないのだけれど、どうせならどんな分布かを図示したいということで、シミュレーションである。

繰り返し乱数を発生させて分布を作る

とりあえず何も考えずに, (1) 2変量正規分布に従う乱数を発生, (2) 相関係数を計算, これをたくさん繰り返す。まぁ10000回ぐらいやってみましょうか。2変量の正規分布に従う乱数の発生にはmvtnormというパッケージを使う。

library(mvtnorm)
size <- 64
mu <- c(0,0)
rho <- 0.8
sigma <- matrix(c(1,rho,rho,1),nrow=2, ncol=2)
sample.cor <- numeric(10000)  # 保存用のベクトル

for (ite.datageneration in 1:10000){
  sample <- rmvnorm(n=size, mean=mu, sigma=sigma)
  sample.cor[ite.datageneration] <- cor(sample[,1],sample[,2])
}

それで計算された10000個の相関係数をヒストグラムにしたものが次の図。サンプルサイズは64で母相関は0.8（図中の赤線）である。

f:id:nekomosyakushimo:20190121001809p:plain

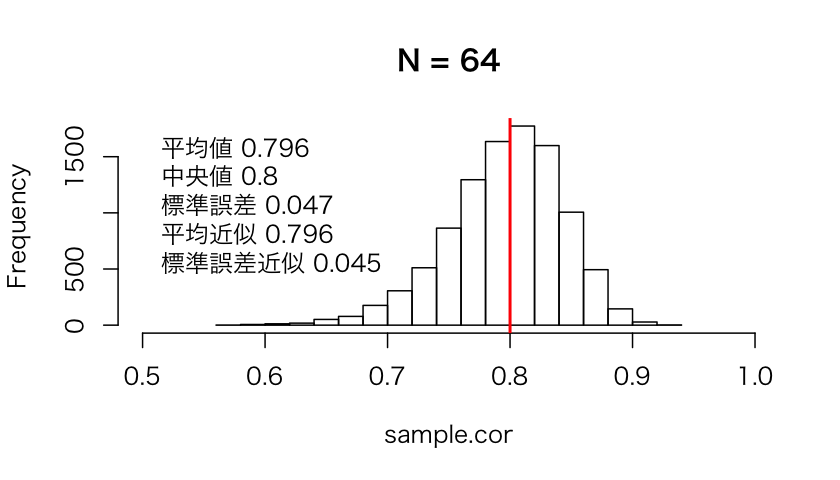
標準誤差の数式から明らかなように, サンプルサイズを増やせば標準誤差は小さくなる。母相関を固定したままNを256, 1024と増やすと次のようになる。

f:id:nekomosyakushimo:20190121001815p:plain

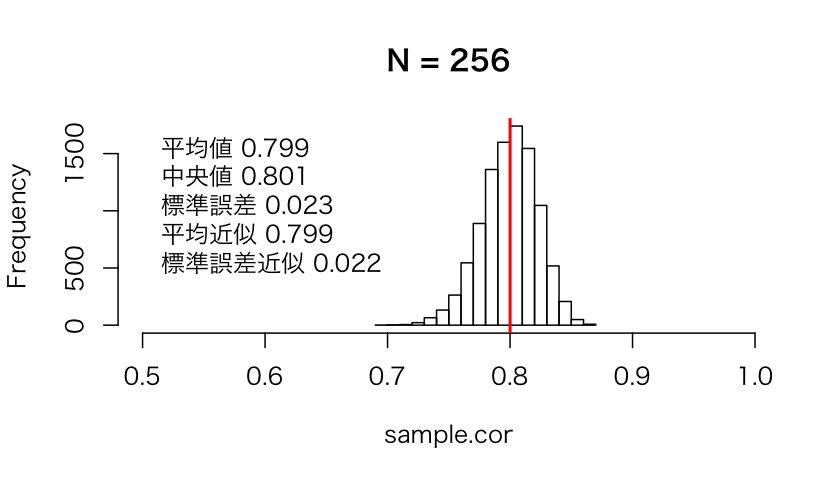
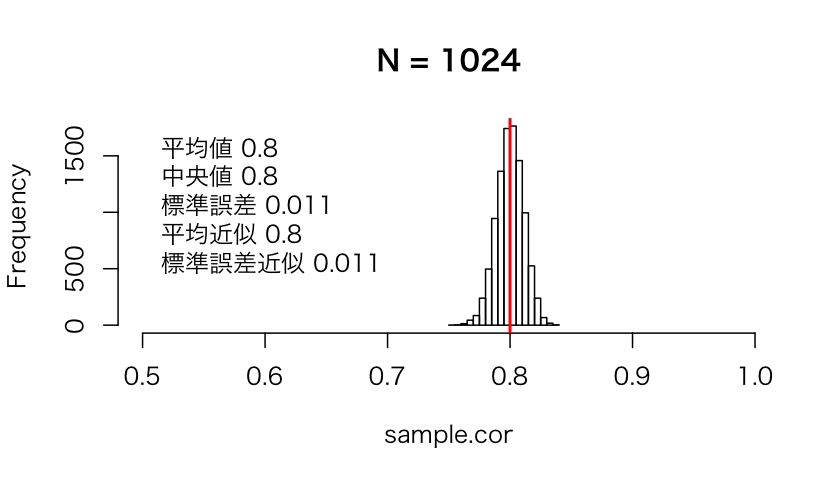
Nが1024だと, かなりの精度はよくなる。

相関係数の標本分布を求める

ところで, 今のは力技シミュレーションによる図示だった訳だが, やはり相関係数の標本分布の確率密度関数をずばっと図示したいのでやってみる。

英語版WikipediaのPearson correlation coefficientの項を見ると, the exact distributionとして載っている。

Pearson correlation coefficient - Wikipedia

f:id:nekomosyakushimo:20190121010115p:plain

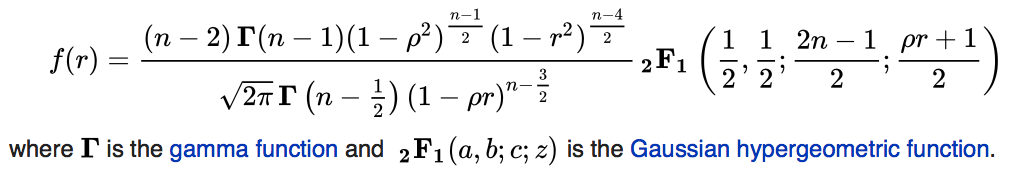
たしかに複雑だ。

$\Gamma$ はガンマ関数で、 $\mathbf {_{2}F_{1}} (a, b; c; z)$ がガウス型超幾何関数だそうだ。とりあえず, 数式を見ながらrでこの式を関数にする。

d.samplecor <- function(r, rho, size){
  shisuu1 <- (size-1)/2
  shisuu2 <- (size-4)/2
  shisuu3 <- size - 3/2

  bunshi <- (size-2) * gamma(size-1) * ((1 - rho^2)^shisuu1) * ((1-r^2)^shisuu2)
  bunbo <- sqrt(2*pi)* gamma(size - 1/2)*((1-rho*r)^shisuu3)
  choukika <- hypergeo(1/2,1/2,(2*size-1)/2,(rho*r+1)/2)

  value <- (bunshi/bunbo) * choukika
  return(Re(value))
}