2017-10-02

必要なサンプルサイズの大きさは（実験編）

前回の記事で、調査を行い母集団における比率を求める際に、誤差を任意の範囲内に収めるための計算について書いた。比率については、

　　 $\displaystyle n = \left( \frac{1.96}{E} \right)^2 p(1-p)$

の式の、Eの部分に収めたい範囲の誤差を代入すると求まることが分かった。

式の上では理論的に求まったものの本当にこれで誤差が所定の範囲内に収まるのか試してみたくなるのが世の常である。ということで、毎度おなじみRを用いたシミュレーションである。

前回の記事で、95%水準で誤差を5%、3%、1%に収めたいときに必要なサンプルサイズは、上の式をそれぞれについて解いて385、1068、9604だと書いた。本当にこの通りになっているか確認してみよう。

まず、二項分布で乱数を発生させる。二項分布の乱数発生の関数はrbinom(n, size, p)である。引数には順番に「観察の回数」「試行の回数」「試行における成功確率」を指定する。今やりたいことに当てはめて考えると、nにはシミュレーションの回数を、sizeにはサンプルサイズを、pには母集団における確率を指定する。シミュレーションの回数はまぁ大体10000回もやればとりあえず良いでしょう。pには計算に用いた0.5を指定しておく。

dat <- rbinom(10000,385,0.5)
head(dat)
# [1] 207 190 198 193 203 185 
length(dat)
# [1] 10000

head関数で中身を除いた結果から分かるように、成功率0.5で385回の試行における成功数についてのデータがそれぞれ発生する。データの個数は当然10000である。

このままだと、比率のデータではないが、サンプルサイズで割るとこれが比率になる。で、ここで得られた標本比率が母集団の比率である50%より5%以上ずれているかを調べたい訳なので、45%より小さいあるいは55%より大きい標本比率の数を数えることにする。その数をシミュレーションの回数で割れば一体何%ぐらいが5%よりも大きな誤差であったかが分かるはずである。

dat <- dat/385
over <- length(dat[dat > 0.55]) + length(dat[dat < 0.45])
over/10000
# [1] 0.0509

結果を見ると分かるように、標本比率の内5%ほどのデータが5%より大きい誤差であることが分かる。逆に言えば、信頼係数である95%の標本は誤差5%以内に収まっているということである。

発生させた比率のデータのヒストグラムは以下のようになる。

f:id:nekomosyakushimo:20171001122622p:plain

正規分布っぽい形をしたこのヒストグラムの両裾が全体の内の5%になる点が、0.45と0.55であるということになろう。

誤差の水準およびサンプルサイズを変えて同様の実験を繰り返し、ヒストグラムを出力したものが次のもの。

f:id:nekomosyakushimo:20171001123034p:plain

f:id:nekomosyakushimo:20171001123045p:plain

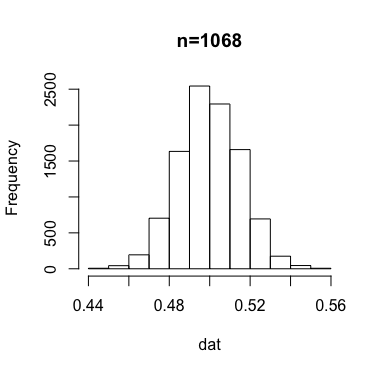
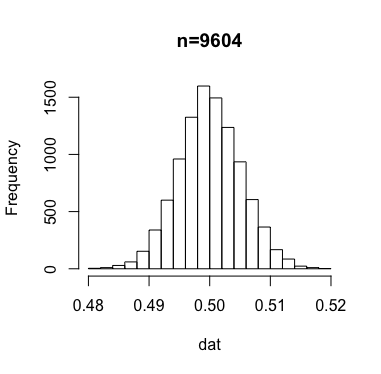
x軸の値に注目していただければ分かるが、サンプルサイズが大きくなるほど、誤差が小さくなっていくのが分かる。それぞれ何パーセントぐらいの結果が、指定した誤差の水準を上回っているかを確認すると、

dat <- rbinom(10000,1068,0.5)
dat <- dat/1068
over <- length(dat[dat > 0.53]) + length(dat[dat < 0.47])
over/10000
# [1] 0.0474

dat <- rbinom(10000,9604,0.5)
dat <- dat/9604
over <- length(dat[dat > 0.51]) + length(dat[dat < 0.49])
over/10000
# [1] 0.0515

やはり5%ぐらいが指定した誤差の水準をオーバーしている。そういう風に値を設定したのだから当然と言えば当然だろうか。微妙に5%とはずれているが、シミュレーションの数を限りなく大きくしていけばこの値は5%に限りなく近づいていくだろう（正確には5%より少しだけ小さい値。サンプルサイズの計算のとき小数点以下を切り上げたから）。

そういえばサンプルサイズの決め方に焦点を当てた本というのがいくつか出ていて、読もう読もうと思って放置していたのだけれど今度どれかを読んでみようかしら。

心理学のためのサンプルサイズ設計入門 (KS専門書)

作者: 村井潤一郎,橋本貴充
出版社/メーカー: 講談社
発売日: 2017/03/08
メディア: 単行本（ソフトカバー）
この商品を含むブログを見る

サンプルサイズの決め方 (統計ライブラリー)

作者: 永田靖
出版社/メーカー: 朝倉書店
発売日: 2003/09/28
メディア: 単行本（ソフトカバー）
購入: 20人クリック: 277回
この商品を含むブログ (14件) を見る

サンプルサイズの設計 (臨床家のための臨床研究デザイン塾テキスト)

作者: 山口拓洋,福原俊一,大西良浩
出版社/メーカー: 特定非営利活動法人健康医療評価研究機構
発売日: 2010/12/01
メディア: 単行本
購入: 1人クリック: 3回
この商品を含むブログ (1件) を見る

2017-10-01

必要なサンプルサイズの大きさは

調べたこと・考えたこと

先日社会調査に関連した話の中で、「完全に無作為抽出が達成されてたとしたらサンプルサイズがどれくらい必要か」についての話になった。「今の首相を支持するかどうか」のようなシンプルな比率の調査をする際にどれくらいのサンプルの大きさがあれば信頼に足るのかを例に考えてみる。

仮に、現在の首相の支持率が母集団において0.3だとする。で、この母集団からn人だけ標本抽出をするのだが、それぞれの人の回答というのが独立していると考えると、これは $B(n, 0.3)$ の二項分布に従うことになる。

二項分布の期待値は $E(x) = np$ であるため、この場合の期待値は $E(x) = 0.3n$ である。10人から回答を得るとすると、支持者は平均的に3人になるし、100人から回答を得るとすると、支持者の数は平均的に30人になる。（平均的にというのは、同じnで標本抽出を繰り返せば28人とか33人とか数値を得ることもあるけど、それらの標本値の分布の平均は30人になるということ。）

続いて二項分布の分散は $V(x) = np(1-p)$ なので、この場合は $V(x) = 0.21n$ になる。そして、その標準偏差は $\sigma (x) = \sqrt{0.21n}$ になる。例えば、100人から回答を得たのであれば $\sigma (x) = \sqrt{21} = 4.582$ となる。

さて今、関心があるのは支持率という比率であるので実現値をnで割ると、

$\displaystyle E\left(\frac{x}{n} \right) = \frac{1}{n}E(x) = p$

となり期待値はpになる。

分散と標準偏差はどうなるかというと $V(ax) = a^2 V(x)$ であるから、

$\displaystyle V(\frac{x}{n}) = \frac{1}{n^2}V(x) = \frac{np(1-p)}{n^2} = \frac{p(1-p)}{n}$

$\displaystyle \sigma(\frac{x}{n}) = \sqrt{\frac{p(1-p)}{n}}$

となる。

ところで、二項分布はnの数が十分に大きければ正規分布で近似ができるのであった。すなわち、標本から得られた比率 $x/n$ は、近似的に $N(p, p(1-p)/n)$ に従う（今求めた期待値と分散）。そこで、信頼係数95%で、

$\displaystyle \frac{\left| \frac{x}{n} - p \right|}{\sqrt{\frac{p(1-p)}{n}}} < 1.96$

である。ここで、推定の誤差を $| x/n - p |$ を一定の値E以内にしようとしたときに、 $| x/n - p | = E$ と置いて上の式に代入し、不等号を=にしてnについて解くと、

$\displaystyle \frac{E}{\sqrt{\frac{p(1-p)}{n}}} = 1.96$

$\displaystyle \frac{E}{1.96} = \sqrt{\frac{p(1-p)}{n}}$

$\displaystyle \left(\frac{E}{1.96}\right)^2 = \frac{p(1-p)}{n}$

$\displaystyle n = \frac{p(1-p)}{(\frac{E}{1.96})^2}$

$\displaystyle n = \left( \frac{1.96}{E} \right)^2 p(1-p)$

が得られる。このEに任意の値を入れることで、確率95%で誤差がEに収まるためのnを求めることができる。

ただ、計算のためにはpの値が必要なのだが、調査を行う前にはこのpが分からないのが普通である（分かっていたのならばそもそも調査などしない！）。 $p(1-p)$ の取りうる最大値は0.25であるので、とりあえず $p=0.5$ にして計算をすれば大きめに標本サイズを見積もることになるが安全だろう。

最初の例にもどり支持率を調査しようと思った場合に、誤差3%に押さえたいとする。Eに0.03を代入すると

$\displaystyle n = \left( \frac{1.96}{0.03} \right)^2 0.5(1-0.5) \simeq 1067.1$

が得られる。すなわち、サンプルサイズを1068以上にすれば、95%の確率で標本から得られた支持率が、母集団における支持率と3%以上離れていないと考えることができる。

ちなみに誤差を5%以内にすると必要なサンプルサイズは385、誤差を1%以内に抑えようとすると9604必要になる。1%単位の誤差で必要なサンプルサイズは結構変わるものである。

ちなみにちなみに、大まかな支持率に当たりが付いているのであれば計算式の $p(1-p)$ のとる値は小さくなるので必要な標本サイズも小さくなる。

【参考】
宮川公男　基本統計学（有斐閣）

基本統計学第4版

作者: 宮川公男
出版社/メーカー: 有斐閣
発売日: 2015/03/30
メディア: 単行本
この商品を含むブログを見る

2017-09-27

バイスプライヤーすごい（セローのエンジンオイル交換に伴うアレコレ）

その他

セローのエンジンオイルを交換したのですが、そのとき想定外に手間取ったことに関するメモ。

手順は下記のサイトを参考にしました。

セロー250メンテナンスオイル交換方法 | セロー250でバイク旅

ただオイルを抜いて入れるだけの話なので難しいこともないはずなのですが、ドレンボルトをソケットレンチで回そうと力を入れるも全然回らず。さらに力を入れるとぐにゃっと嫌な感触とともにレンチが回り、ボルトの頭をなめてしまっています。

そこからは、ボルトを回そうと力を入れるとボルトをなめる一方で、一向にボルトは緩まず。

グーグル先生に聞いたところによれば、似たような事態に陥っているケースはままあるようです。

なめてしまったボルトのはずし方教えてください。 - バイクの... - Yahoo!知恵袋
 ルート5 : なめったボルトとナットツイスター
 WR250Xのオイル交換！純正ドレンボルトはナメりやすいので初心者は注意！ | WR250Xで進行形！

で、手持ちの工具だとどうにもならなそうだったので、上記の体験談を参考に一番安く済みそうなバイスプライヤーを近くのホームセンターで購入して、なんとかすることに。

バイスプライヤーってのは、ロッキングプライヤーとも言われたりすることもある、

トップ(TOP) バイスプライヤ VP-125

出版社/メーカー: トップ工業
メディア: Tools & Hardware
クリック: 5回
この商品を含むブログを見る

こんな工具のことで、挟んだものをかなり強固に固定できるものだそうです。ホームセンターのプライベートブランドの安物で700円程度でした。

あと、ドレンボルトは交換が必要なので、ネットで評判が良さそうだった

キジマ(Kijima) ワイヤーロックドレンボルト 105-112

出版社/メーカー: キジマ(Kijima)
発売日: 2012/11/16
メディア: Automotive
この商品を含むブログを見る

これを注文しました。ボルトの頭が純正よりかはかなり大きいので今後なめる心配もなさそうです。（ワイヤーでロックもできるそうですが、私はレースに出るとかとは関係ないのでワイヤーはつけていません。）

で、バイスプライヤーでがっちりとボルトを固定して力を加えると、思ったよりあっさりと回ってくれて無事になめてしまったドレンボルトをはずすことに成功。その後は特に困ることもなくいつも通りの手順で交換できました。

問題となっていたドレンボルト。

f:id:nekomosyakushimo:20170927160910j:plain

六角形の角がつぶれて丸みを帯びてきています（レンチで力づくで何度か回したから）。ギザギザしているのはバイスプライヤーが食い込んだ部分です。がっちりと噛んで固定したことが分かります。

2017-09-22

二項分布の4次のモーメントの導出

調べたこと・考えたこと

前回までで3次のモーメントをやったんだから次は4次だろう（安易）。

nekomosyakushimo.hatenablog.com
nekomosyakushimo.hatenablog.com

原点まわりのモーメントの導出

まず、モーメント母関数を3回微分したのものがこちら。

　　 $\begin{split} f^{\prime\prime\prime}(\xi) &= np \{ (n-1) 2pe^{2\xi}(pe^\xi + q)^{n-2} + (n-1)(n-2)p^2e^{3\xi}(pe^\xi +q)^{n-3}\\ \\ &\quad + e^\xi (pe^\xi + q)^{n-1} + (n-1)pe^{2\xi} (pe^\xi + q)^{n-2} \} \end{split}$

これを、（大変に面倒くさいけど）さらにもう1回微分すると、

　　 $\begin{split} f^{\prime\prime\prime\prime}(\xi) &= np \{ 4(n-1)pe^{2\xi} (pe^\xi + q)^{n-2} + 2(n-1)(n-2)p^2e^{3\xi}(pe^\xi +q)^{n-3}\\ \\ &\quad + 3(n-1)(n-2)p^2 e^{3\xi}(pe^\xi + q)^{n-3} + (n-1)(n-2)(n-3) p^3e^{4\xi} (pe^\xi + q)^{n-4} \\ \\ &\quad + e^\xi(pe^\xi + q)^{n-1} + (n-1) pe^{2\xi}(pe^\xi + q)^{n-2} \\ \\ &\quad + 2(n-1) pe^{2\xi}(pe^\xi + q)^{n-2} + (n-1)(n-2) p^2e^{3\xi}(pe^\xi + q)^{n-3} \} \end{split}$

このような形になる。次に、 $\xi =0$ とおき、次数を揃えながら整理していくと、

　　 $\begin{split} f^{\prime\prime\prime\prime}(0) &= np \{ 4(n-1)p + 2(n-1)(n-2)p^2 + 3(n-1)(n-2)p^2 + (n-1)(n-2)(n-3) p^3 \\ \\ &\quad + 1 + (n-1) p + 2(n-1) p + (n-1)(n-2) p^2 \}\\ \\ &= np \{ (n-1)(n-2)(n-3) p^3 + [(n-1)(n-2) + 2(n-1)(n-2) + 3(n-1)(n-2) ] p^2 \\ \\ &\quad + [ 4(n-1) + 2(n-1) + (n-1)]p + 1 \}\\ \\ &= np \{ (n-1)(n-2)(n-3) p^3 + 6(n-1)(n-2)p^2 + 7(n-1)p + 1 \} \\ \\ &= n(n-1)(n-2)(n-3) p^3 + 6n(n-1)(n-2)p^3 + 7n(n-1)p^2 + np \end{split}$

が求まる。これが二項分布の4次の原点まわりのモーメントである。

平均値まわりのモーメントの導出

次に、平均値まわりでのモーメントを求めてみよう。求める値は、

　　 $\displaystyle \begin{split} m_4 &= E\big( (x - \mu)^4 \big) = E(x^4 -4x^3 \mu + 6x^2\mu^2 -4x\mu^3 + \mu^4 )\\ \\ &= E(x^4) -4\mu E(x^3) + 6\mu^2 E(x^2) -4\mu^3 E(x) + \mu^4 \\ \\ &= E(x^4) -4\mu E(x^3) + 6\mu^2 E(x^2) -3\mu^4 \end{split}$

である。各項に原点まわりのモーメントを代入すると、

　　 $\begin{split} m_4 &= n(n-1)(n-2)(n-3)p^4 + 6n(n-1)(n-2)p^3 + 7n(n-1)(n-2)p^2 + np \\ \\ & \quad - 4np\{n(n-1)(n-2)p^3 + 3n(n-1)p^2 + np\} + 6n^2p^2 \{n(n-1) + np\} -3n^4p^4 \end{split}$

となる。とりあえず強引に全部展開すると、

　　 $\begin{split} m_4 &= n(n-1)(n-2)(n-3)p^4 + 6n(n-1)(n-2)p^3 + 7n(n-1)(n-2)p^2 + np \\ \\ & \quad - 4n^2(n-1)(n-2)p^4 -12n^2(n-1)p^3 -4n^2p^2 + 6n^3(n-1)p^4 +6 n^3p^3 -3n^4p^4 \end{split}$

になり、それを $p$ の次数で整理すると、

　　 $\begin{split} m_4 &= (3n^2 -6n)p^4 + (-6n^2 +12n)p^3 + (3n^2 -7n)p^2 + np \end{split}$

が得られる。3次までの平均まわりのモーメントでは、 $np$ および $(1-p)$ が登場していたことに注意をしつつ、これを因数分解していくと、

　　 $\begin{split} m_4 &= (3n^2 -6n)p^4 + (-6n^2 +12n)p^3 + (3n^2 -7n)p^2 + np \\ \\ &= 3n^2p^4 - 6np^4 -6n^2p^3 + 12np^3 + 3n^2p^2 - 7np^2 + np \\ \\ &=np\{ 3np^3 - 6p^3 -6np^2 + 12p^2 + 3np - 7p + 1 \}\\ \\ &=np\{ 3np^3 - 6np^2 + 3np - 6p^3 + 12p^2 - 6p + 1 - p \}\\ \\ &=np\{ 3np(p^2 - 2p + 1) -6p (p^2 -2p + 1) + 1 - p \}\\ \\ &=np\{ 3np(1 - p)^2 -6p (1 - p)^2 + 1 - p \} \\ \\ &=np\{ (3np -6p)(1 - p)^2 + 1 - p \} \\ \\ &=np(1-p)\{(3np -6p)(1 - p) + 1 \} \\ \\ &=np(1-p)\{1+ 3(n - 2)p(1 - p)\} \end{split}$

が求まる。これが、平均まわりの4次のモーメントである。非常に煩雑な計算であった。

2017-09-21

続・二項分布の3次のモーメント

調べたこと・考えたこと

前回の記事で、モーメント母関数を用いた二項分布の3次のモーメントの導出について書いた。今回は、二項分布から抽出したデータの分布を実際に見ながら3次のモーメントと分布の形にについてみてみる。

Rのデフォルトの関数には、歪度を計算するものはないらしい。momentsというパッケージを入れれば、その中にskewness()という歪度を計算する関数があるので今回はそれを使う。

まずは、成功確率 $p$ が異なる二項分布から、それぞれ $n = 1000$ 程度でデータを発生させる。

dat1 <- rbinom(1000,10,prob=0.5 )
dat2 <- rbinom(1000,10,prob=0.25)
dat3 <- rbinom(1000,10,prob=0.75)
dat4 <- rbinom(1000,10,prob=0.10)
dat5 <- rbinom(1000,10,prob=0.90)

それぞれのデータで歪度を求めるとともに、度数分布をプロットしてみる。

まずは、 $p= 0.5$ のものから。

f:id:nekomosyakushimo:20170915225523p:plain

$a_3 = -0.0515$ で、0に近い。分布もそれに対応して概ね左右対称である。

続いて、 $p= 0.25$ のものを見る。

f:id:nekomosyakushimo:20170915225731p:plain

$a_3 = 0.373$ である。歪度は正の値だと、右の裾が長くなると言われており、分布からも確認することができる。

今度は、 $p = 0.75$ 。

f:id:nekomosyakushimo:20170915230344p:plain

$a_3 = -0.382$ であり、負の値なので左の裾が長くなっている。一つ前のものと比べると絶対値は似たような値であり、分布の歪みの程度が大体同じであることを示している。

より偏りのある $p= 0.10$ で見てみよう。

f:id:nekomosyakushimo:20170915230750p:plain

$a_3 = 0.991$ であり、より大きな偏りを持ち、右の裾の長い分布であることが分かる。

最後は $p= 0.90$ 。

f:id:nekomosyakushimo:20170915231059p:plain

$a_3 = - 0.899$ で、予想通りに左に裾が長い分布が確認できる。

歪度を求めると分布の形についてより詳細に分かるので、分布の形状を確かめるときには算出すると良いでしょう。

2017-09-20

二項分布の3次のモーメント

調べたこと・考えたこと

統計学の教科書において確率分布を紹介するときに2次のモーメントまでしか載っていないことが多い。

モーメント母関数を用いれば、何次のモーメントでも求めることができるので、何の役に立つかは分からないが、ここでは二項分布の3次のモーメントを求めてみよう。

n次のモーメントの求め方は、モーメント母関数を $n$ 回微分して、 $\xi$ を0と置くのであった。まず、二項分布のモーメント母関数を2階微分をしたものは、

　　 $f^{\prime\prime}(\xi) = np \{ (n-1) pe^{2\xi}(pe^\xi + q)^{n-2} + e^\xi(pe^\xi + q)^{n-1} \}$

である。これをさらに微分すると、

　　 $\begin{split} f^{\prime\prime\prime}(\xi) &= np \{ 2pe^{2\xi}(n-1) (pe^\xi + q)^{n-2} + p^2e^{3\xi}(n-1)(n-2)(pe^\xi +q)^{n-3}\\ \\ &\quad + e^\xi (pe^\xi + q)^{n-1} + pe^{2\xi} (n-1)(pe^\xi + q)^{n-2} \} \end{split}$

となる。そこで、 $\xi =0$ とおき、 $p$ の次数で整理すると、

　　 $\begin{split} f^{\prime\prime\prime}(0) &= np \{ 2p(n−1) + p^2(n−1)(n−2)+ 1 + p(n−1) \} \\ \\ &= 2np^2(n−1)+np^3(n−1)(n−2)+np+np^2 (n−1)\\ \\ &= n(n−1)(n−2)p^3 + 3n(n−1)p^2 + np \end{split}$

となり原点まわりの3次のモーメントが得られる。これを利用し、今度は平均値周りの3次のモーメントを求めてみる。平均値周りのモーメントは、

　　 $m_3 = E((x - \mu)^3)$

であり、これを展開すると、

　　 $m_3 = E(x^3) -3\mu E(x^2) + 2\mu^3$

となる。 $\mu = E(x) = np$ であるので、先に求めた原点まわりのモーメントをこの式に代入することで、 $m_3$ を求めることができる。ちなみに、2次の原点周りのモーメントは、

　　 $E(x^2) = n(n-1)p^2 + np$

である。

まず、それぞれを代入する。

　　 $\begin{split} m_3 &= n(n−1)(n−2)p^3 + 3n(n−1)p^2 + np -3np \{ n(n-1)p^2 + np \} + 2n^3p^3\\ \\ &= np \{ (n−1)(n−2)p^2 + 3(n−1)p + 1 - 3(n-1)np^2 -3np + 2n^2p^2 \} \end{split}$

ごちゃごちゃしていて分かりづらいが、{ }の中を $p$ の次数にそって整理し、各係数を計算していくと、

　　 $\begin{split} m_3 &= np \{ (n−1)(n−2)p^2 + 3(n−1)p + 1 - 3(n-1)np^2 -3np + 2n^2p^2 \} \\ \\ &= np \{ \{(n−1)(n−2)- 3(n-1)n + 2n^2 \}p^2 + \{3(n−1) - 3n \} p + 1 \} \\ \\ &= np (2p^2 - 3p +1)\\ \\ &= np (1 - p)(1 - 2p) \end{split}$

が求まる。

3次のモーメントを標準偏差の3乗 $\sigma^3$ で割ったものは歪度と呼ばれて分布の左右対称性の指標とされたりする。 $q = (1-p)$ とすると分散は $npq$ 、 $\sigma = \sqrt{npq}$ と表せるので、

　　 $\displaystyle 歪度 = \frac{m_3}{\sigma^3} = \frac{npq(1 - 2p)}{(\sqrt{npq})^3} = \frac{npq(1 - 2p)}{npq \sqrt{npq}} = \frac{1 - 2p}{ \sqrt{npq}}$

となる。分子に注目すると、 $p =0.5$ のときに歪度は0となることがわかる。 $p > 0.5$ では、歪度は負の値をとり、 $p < 0.5$ では歪度は正の値をとる。歪度が0のときに分布は左右対称で、歪度が正のときには右の裾が長く、負のときには左の裾が長い分布が得られる。実際に二項分布の確率分布を確認してみてもその通りになっていることが分かる。

2017-09-19

モーメントについて

調べたこと・考えたこと

モーメントについての学習メモ。

モーメント（積率）という概念がある。これは、確率分布の性質のうちのいくつかを数値で表したものである。平均値や分散というのもモーメントの一種である。

離散値をとる確率変数 $x$ について、その確率分布を $P(x)$ としたときに、 $x^n$ の期待値を $x$ の確率分布の $n$ 次のモーメントという。

　　　 $\acute{m}_n = E(x^n) = \sum_x x^n P(x)$

これは、原点まわりのモーメントと呼ばれたりする。 $n=1$ である1次のモーメントはそのまま定義通りに平均値である。

一般にモーメントが用いられるのは平均値のまわりらしく、確率変数 $x$ と $\mu$ の差のべき指数で求められるモーメントである。

　　　 $m_n = E \big( (x - \mu)^n \big) = \sum_x (x - \mu)^n P (x)$

こういったものを平均値のまわりの $n$ 次のモーメントと呼ぶ。原点まわりと平均値まわりをここでは $\prime$ の有無で区別する。平均値まわりの1次のモーメントを求めると以下のようになる。（ここで、 $\sum_x P(x)$ は確率の定義から1である。※サイコロのすべての目の確率は足すと1。）

　　　 $m_1 = \sum_x (x -\mu)P(x) = \sum_x xP(x) -\mu \sum_x P(x) = \mu - \mu = 0$

平均値まわりの２次のモーメント（つまりは分散）を計算するには、定義式のものより原点まわりのモーメントを用いて次のように計算すると簡単らしい。

　　　 $m_2 = \acute{m}_2 - \mu^2 = E(x^2) - \mu^2$

これは何かというと、分散の簡便な計算式とされる「2乗の平均 - 平均の2乗」にほかならない。

さて、モーメントを求める際には、モーメントを生み出すモーメント母関数というものを用いると便利であるらしい。モーメント母関数とは $\xi$ (グザイとかクシーと読む)についての次のような関数である。

　　　 $f(\xi) = E (e^{\xi x})$

指数関数の級数展開の公式というものがあり、

　　　 $\displaystyle e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \dots$

これを用いると、モーメント母関数の式は、

　　　 $\displaystyle f(\xi) = E \big( 1 + \xi x + \frac{\xi^2 x^2}{2!} + \frac{\xi^3 x^3}{3!} + \dots \big)$

このようになる。さらに式を変形すると、

　　　 $\displaystyle f(\xi) = 1 + \xi E(x) + \frac{\xi^2}{2!} E(x^2)+ \frac{\xi^3}{3!} E(x^3) + \dots$

このようになり、これを最初に紹介した原点まわりのモーメントで置き換えると、

　　　 $\displaystyle f(\xi) = 1 + \xi \acute{m}_1 + \frac{\xi^2}{2!} \acute{m}_2+ \frac{\xi^3}{3!} \acute{m}_3 + \dots$

が得られる。展開式の係数に次々と高次のモーメントが現れてくる。この母関数を用いると、面倒な計算を避けてお目当てのモーメントを計算することができるというのだ。

$n$ 次の原点まわりのモーメント $\acute{m}_n$ を求めたいのであれば、 $f(\xi)$ を $\xi$ について $n$ 回微分をし、 $\xi = 0$ とすれば求められる。先に求めた展開式を見れば分かるように、 $\xi = 0$ とすることで、 $n$ よりも右の項はすべて0になるので目当てとするモーメントだけが取り出せるわけである。

二項分布を例にして考えてみよう。二項分布の確率関数は次の式で表される。

　　　 $P(x) = {}_n C _x p^x q^{n-x}$

まずは、これをモーメント母関数に埋め込み、多少の変形を行う。

　　　 $\begin{equation*} \begin{split} f(\xi) &= \sum_{x=0} ^n e^{\xi x} P(x) \\ &= \sum_{x=0} ^n e^{\xi x} {}_n C _x p^x q^{n-x}\\ &= \sum_{x=0} ^n {}_n C _x (pe^\xi)^x q^{n-x} \end{split} \end{equation*}$

最右辺の式は、二項定理を用いると次のように書くことができる。

　　　 $f(\xi) = (q + pe^\xi)^n$

この式を用いて、 $\acute{m}_1$ を求める。1次のモーメントなので、1回微分を行い、 $\xi = 0$ とおく。（ $(p+q)$ は1、および、eの0乗は1なことから、下から２番目の式の（）内は1である）

　　 $\begin{equation*} \begin{split} \acute{m}_1 &= \frac{df(\xi)}{d\xi}\\ &= npe^\xi(q + pe^\xi)^{n-1} \\ f^{\prime}(0) &= np \end{split} \end{equation*}$

二項分布の平均値である、 $np$ が無事に算出された。続いて、 $\acute{m}_2$ を求めてみよう。まず、2階微分を行う。

$\begin{equation*} \begin{split} \acute{m}_2 &= \frac{d^2f(\xi)}{d\xi^2}\\ &= npe^\xi \big((n-1)(q + pe^\xi)^{n-2} pe^\xi\big) + npe^\xi (q + pe^\xi)^{n-1}\\ &= npe^\xi \big( (n-1)(q + pe^\xi)^{n-2} pe^\xi + (q + pe^\xi)^{n-1} \big)\\ \end{split} \end{equation*}$

そして、 $\xi = 0$ とすると、

$\begin{equation*} \begin{split} f^{\prime\prime}(0) &= np \big( (n-1) p + 1 \big)\\ &= np (np + 1 - p ) \\ &= np (np + q ) \\ &= n^2p^2 + npq\\ \end{split} \end{equation*}$

$\acute{m}_2 = n^2p^2 + npq$ が得られる。あとは、最初の方に述べたように、原点まわりのモーメントから平均の2乗、すなわち $n^2p^2$ を引くことで、

　　　 $m_2 = npq$

が得られる。二項分布の分散も無事に算出された。

このように、モーメント母関数を用いれば様々な確率分布のモーメントを求めることができる。

【参考】
『キーポイント確率・統計』（岩波書店）

猫も杓子も構造化

発達障害、特別支援などについて書いています。最近は心理学関係の内容が多めです。

必要なサンプルサイズの大きさは（実験編）

必要なサンプルサイズの大きさは

バイスプライヤーすごい（セローのエンジンオイル交換に伴うアレコレ）

二項分布の4次のモーメントの導出

原点まわりのモーメントの導出

平均値まわりのモーメントの導出

続・二項分布の3次のモーメント

二項分布の3次のモーメント

モーメントについて