猫も杓子も構造化

発達障害、特別支援などについて書いています。最近は心理学関係の内容が多めです。

相関係数の標本分布について

R

はじめに

『心理統計学の基礎』のp.114に相関係数の標本分布が図示されている。確率密度関数は数学的にかなり複雑だからとの理由で省略される代わりに近似的にその期待値を求める式が載っている。

\displaystyle{ \mu_r = \rho - \frac{ \rho (1- \rho^2)}{2N} }

その標本誤差についてもやはり近似的に求める次のような式が載っている。

\displaystyle{ \sigma_r = \frac{ 1- \rho^2}{\sqrt{N}} }

これらの近似的なものでもさして困らないのだけれど、どうせならどんな分布かを図示したいということで、シミュレーションである。

繰り返し乱数を発生させて分布を作る

とりあえず何も考えずに, (1) 2変量正規分布に従う乱数を発生, (2) 相関係数を計算, これをたくさん繰り返す。まぁ10000回ぐらいやってみましょうか。2変量の正規分布に従う乱数の発生にはmvtnormというパッケージを使う。

library(mvtnorm)
size <- 64
mu <- c(0,0)
rho <- 0.8
sigma <- matrix(c(1,rho,rho,1),nrow=2, ncol=2)
sample.cor <- numeric(10000)  # 保存用のベクトル

for (ite.datageneration in 1:10000){
  sample <- rmvnorm(n=size, mean=mu, sigma=sigma)
  sample.cor[ite.datageneration] <- cor(sample[,1],sample[,2])
}

それで計算された10000個の相関係数をヒストグラムにしたものが次の図。サンプルサイズは64で母相関は0.8（図中の赤線）である。

f:id:nekomosyakushimo:20190121001809p:plain

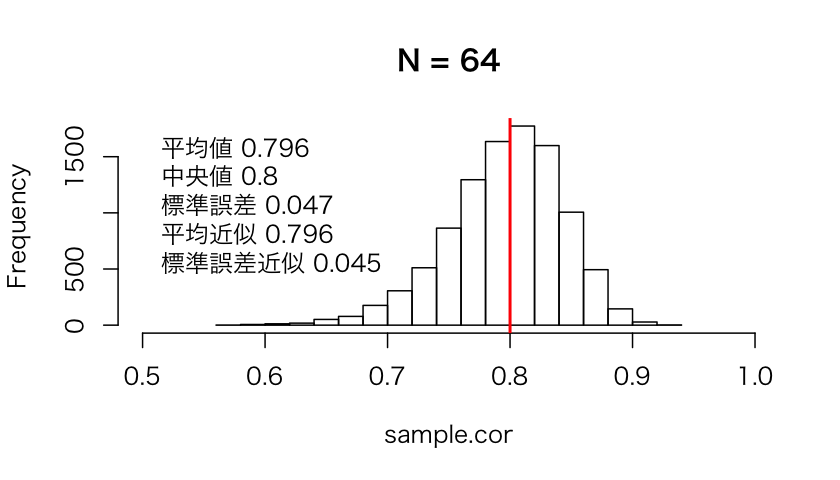
標準誤差の数式から明らかなように, サンプルサイズを増やせば標準誤差は小さくなる。母相関を固定したままNを256, 1024と増やすと次のようになる。

f:id:nekomosyakushimo:20190121001815p:plain f:id:nekomosyakushimo:20190121001825p:plain

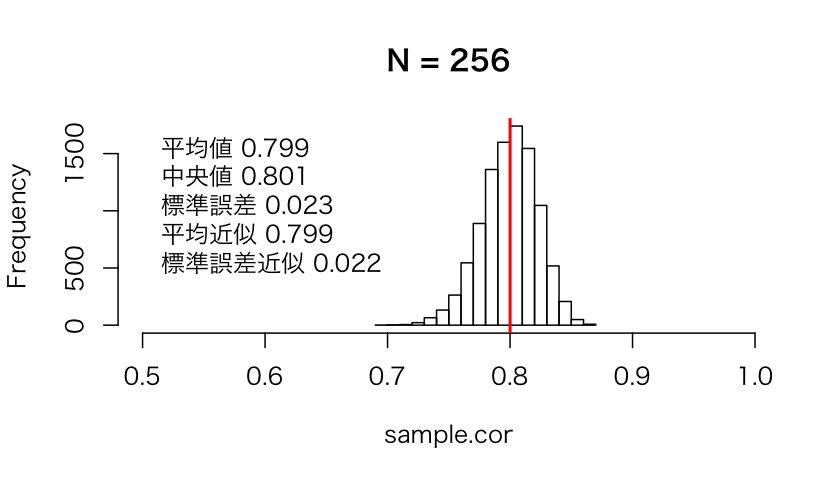
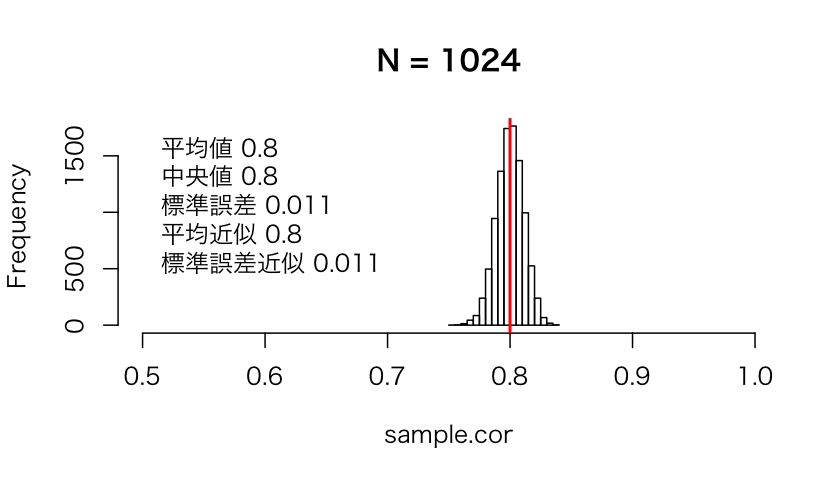
Nが1024だと, かなりの精度はよくなる。

相関係数の標本分布を求める

ところで, 今のは力技シミュレーションによる図示だった訳だが, やはり相関係数の標本分布の確率密度関数をずばっと図示したいのでやってみる。

英語版WikipediaのPearson correlation coefficientの項を見ると, the exact distributionとして載っている。

Pearson correlation coefficient - Wikipedia

f:id:nekomosyakushimo:20190121010115p:plain

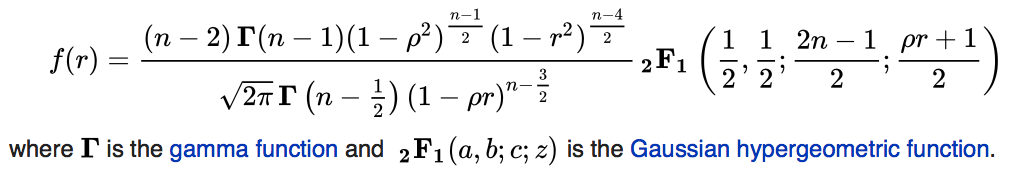
たしかに複雑だ。

\Gamma はガンマ関数で、 \mathbf {_{2}F_{1}} (a, b; c; z) がガウス型超幾何関数だそうだ。とりあえず, 数式を見ながらrでこの式を関数にする。

d.samplecor <- function(r, rho, size){
  shisuu1 <- (size-1)/2
  shisuu2 <- (size-4)/2
  shisuu3 <- size - 3/2

  bunshi <- (size-2) * gamma(size-1) * ((1 - rho^2)^shisuu1) * ((1-r^2)^shisuu2)
  bunbo <- sqrt(2*pi)* gamma(size - 1/2)*((1-rho*r)^shisuu3)
  choukika <- hypergeo(1/2,1/2,(2*size-1)/2,(rho*r+1)/2)

  value <- (bunshi/bunbo) * choukika
  return(Re(value))
}

超幾何関数を扱うにはそのものずばりなhypergeoというパッケージがあるらしくてその中にあるhypergeo関数を使っている。これをインストールしないと途中で止まる。

で, この関数-1から1までの範囲でとりあえず積分してみる。

f:id:nekomosyakushimo:20190121002059p:plain

計算の結果は誤差が0.000072で近似値が1である。面積が1になったということで, とりあえず確率密度関数にはなったのかな？

これを, さっきのシミュレーションのヒストグラムに重ねてみると, どうやらちゃんと確率密度関数になっているっぽい。

f:id:nekomosyakushimo:20190121002033p:plain f:id:nekomosyakushimo:20190121002047p:plain

同じサンプルサイズでも母相関係数が違うと分布の精度はだいぶ違うものですね。

という訳で、無事に相関係数の標本分布の確率密度関数を図示することに成功した。というかなんで、自分はこんなことをやり始めたのだろうか？

ちなみに, この関数サンプルサイズが172ぐらいまでだと正しく計算できるけれど, それを越した場合にはガンマ関数の値が大きくなりすぎて計算不能になるのでご注意を。

『心理職のためのエビデンス・ベイスト・プラクティス入門』

読んだ本

心理職のためのエビデンス・ベイスト・プラクティス入門―エビデンスを「まなぶ」「つくる」「つかう」

心理職のためのエビデンス・ベイスト・プラクティス入門―エビデンスを「まなぶ」「つくる」「つかう」

近年、エビデンスという言葉をよく聞くようになった。しかし、その言葉が何を意味するのかということについて共通の理解がないままに使われるような場面にもよく出くわす。とりあえず何かしらの数量的なものが示されればそれがエビデンスだ、という人も見る。

この本は、エビデンス・ベイスドについて、心理職を対象に平易な言葉で解説している。エビデンスとはそもそも何であるのか（まなぶ）、どのようにエビデンスが産み出されるのか（つくる）、臨床に携わる心理職はどのようにエビデンスを活用すれば良いのか（つかう）、というように、心理職がエビデンスと関わる足場を提供してくれる。臨床家にも研究者にも役に立つ本だと思う。

丁寧な言葉でかかれた解説書であるが、精神力動学的アプローチを中心とした日本の臨床心理学については、ガラパゴス化していると結構手厳しい。

アセスメントの選択にしても、介入法の選択にしても「自分が習った」あるいは「自分が得意とする」ものに偏りがちなのは心理職も人間である以上しかたがないような気がするけれども、そうしたところと離れてエビデンスを吟味することがこれから必要になっていくのであろう。そのためには、メタ・アセスメント論とかメタ・介入法みたいな議論が必要なのではないかと、そんなことを考えながら読んでいた。

猫も杓子も今年の3冊【2018年】

全く余裕がなくて記事の更新がストップしているけれど, 年一で書いているシリーズものぐらいは更新しておこうかと思います。

過去のもの

猫も杓子も今年の3冊【2017年】 - 猫も杓子も構造化
猫も杓子も今年の３冊【2016年】 - 猫も杓子も構造化
猫も杓子も今年の３冊【2015年】 - 猫も杓子も構造化

心理学関係

おさなごころを科学する: 進化する幼児観

おさなごころを科学する: 進化する幼児観

発達関連について学ぶことが多い1年だった。SENSのセミナーなんかだと, 発達障害を理解するために「とりあえず定型発達の道筋をみましょう」みたいなノリでピアジェとかが紹介されたりする印象があるけれども, ピアジェ以降の発達心理学が何を積み上げてきたかについて言及されることは少ない。本書は著者のブログをリライトしたもので, 非専門家である人でも読みやすいし, 引用がしっかりとされているので, ここを入り口にさらに調べていくことも可能である。

障害児教育関係

障害児の発達臨床〈1〉感覚と運動の高次化からみた子ども理解

障害児の発達臨床〈1〉感覚と運動の高次化からみた子ども理解

発達というととかく認知面を解説する本が多いが, この本は発達の中心に感覚と運動を据えている点で大変ユニーク。著者の臨床経験に基づく独自の理論が展開されている。臨床のアイディアは豊富に得られると思う。

統計関係

調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)

調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)

調査観察データを扱うことはあまりないのですがお勉強として。非実験系のデータで因果推論をしたい人は必読に思う。

みなさま良いお年を。

確認的因子分析の際のモデルの識別についての調べ物

調べたこと・考えたこと

必要があってモデルの識別についての調べ物をしたその覚書。 使うデータはおなじみHolzingerSwineford1939。

潜在変数間に相関を仮定しない次のようなモデルを作ってみる。

library(lavaan)

dat <- HolzingerSwineford1939

model1 <-"
A =~ x1 + x2
B =~ x4 + x5 + x6
C =~ x7 + x8 + x9
A ~~ 0*B
A ~~ 0*C
B ~~ 0*C
"

res1 <- cfa(model1,dat=dat)

このときに、観測変数が2つだけ（潜在変数Aの部分）だとモデルが識別できないとエラーを吐く。

警告メッセージ:
lav_model_vcov(lavmodel = lavmodel, lavsamplestats = lavsamplestats,  で:
 lavaan WARNING:
   Could not compute standard errors! The information matrix could
   not be inverted. This may be a symptom that the model is not
   identified.

エラーメッセージの通り標準誤差が算出されない。

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)
  A =~                                                
    x1                1.000                           
    x2                0.661       NA                  
  B =~                                                
    x4                1.000                           
    x5                1.133       NA                  
    x6                0.924       NA                  
  C =~                                                
    x7                1.000                           
    x8                1.225       NA                  
    x9                0.854       NA

ミューテン先生によると次のようなことが原因だと。（これはbifactorモデルについてのところでの説明）

When specific factors have only 2 indicators you cannot identify the loading for the second of those indicators. Think of the specific factor as absorbing a residual correlation between those 2 indicators - there is only 1 such correlation and therefore you can only identify 1 parameter, in this case the specific factor variance.

Bifactor Model Problems

これを潜在変数間に相関を仮定した次のようなモデルにすると識別エラーは解決する。

model2 <-"
A =~ x1 + x2
B =~ x4 + x5 + x6
C =~ x7 + x8 + x9
"

res2 <- cfa(model2,dat=dat)

ちゃんと標準誤差も算出できている。

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)
  A =~                                                
    x1                1.000                           
    x2                0.438    0.129    3.401    0.001
  B =~                                                
    x4                1.000                           
    x5                1.113    0.065   17.073    0.000
    x6                0.923    0.055   16.708    0.000
  C =~                                                
    x7                1.000                           
    x8                1.180    0.165    7.175    0.000
    x9                1.018    0.141    7.205    0.000

潜在変数が無相間だから、Aの部分だけで考えると、p(p+1)/2 = 3 （pは観測変数の数）で、ここから推定する母数の数を引いた値がプラスにならないとモデルが識別されないこととなる。で、最初のモデル1だと潜在変数からのパス1本と残差の分散２つでの3つの母数を推定しているので, 3-3=0となりこれがいかんようだ。制約を例えば次のように足してみると無事に識別される。

model3 <-"
A =~ x1 + x2
B =~ x4 + x5 + x6
C =~ x7 + x8 + x9
A ~~ 0*B
A ~~ 0*C
B ~~ 0*C
x1~~1*x1
"

res3 <- cfa(model3,dat=dat)

標準誤差もちゃんと計算されている。

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)
  A =~                                                
    x1                1.000                           
    x2                1.137    0.333    3.410    0.001
  B =~                                                
    x4                1.000                           
    x5                1.133    0.067   16.906    0.000
    x6                0.924    0.056   16.391    0.000
  C =~                                                
    x7                1.000                           
    x8                1.225    0.190    6.460    0.000
    x9                0.854    0.121    7.046    0.000

とりあえずここまで。

ここのところの読書

読んだ本

忙しいので記事にするだけのまとまった時間がとれないのですが、（後の自分のための）読んだという記録だけでも。

障害児の発達臨床〈1〉感覚と運動の高次化からみた子ども理解

障害児の発達臨床〈1〉感覚と運動の高次化からみた子ども理解

もっと早く読むべきだった。そのうち記事にする。

日本版DN-CASの解釈と事例

日本版DN-CASの解釈と事例

主に仕事の必要性で読んだ。この本の出版で心理臨床にはだいぶ使いやすくなったんだろう（多分）。

教師と学校が変わる学校コンサルテーション (ハンディシリーズ 発達障害支援・特別支援教育ナビ)

教師と学校が変わる学校コンサルテーション (ハンディシリーズ 発達障害支援・特別支援教育ナビ)

これも仕事の都合。コンパクトだけれども外部から学校に関わる人は読んで損はないと思う。

統計思考の世界 ~曼荼羅で読み解くデータ解析の基礎

統計思考の世界 ~曼荼羅で読み解くデータ解析の基礎

統計学の世界における分析と分析のつながりが曼荼羅で可視化されていて良い。最初の１冊ではないとは思うが、ある程度学んで色々としっくりきていない人は勉強になると思う。

調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)

調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)

大変勉強になる読書。調査観察データから因果推論やりたい人は必読。

完璧な親なんていない!―カナダ生まれの子育てテキスト

完璧な親なんていない!―カナダ生まれの子育てテキスト

  • 作者: ジャニス・ウッドキャタノ,三沢直子,Janice Wood Catano,幾島幸子
  • 出版社/メーカー: ひとなる書房
  • 発売日: 2002/08/01
  • メディア: 単行本
  • 購入: 1人 クリック: 18回
  • この商品を含むブログ (7件) を見る

カナダで無料で親に配布される子育て小冊子をまとめたもの。これも仕事の都合で読んだ。親が子育てに追い詰められないために必要な基礎的な知識から具体的な方法まで。「親だって人間です」からスタートするのがいいですね。

Fisher流とNeyman-Pearson流とp値と心理学と

論文メモ

www.jstage.jst.go.jp

日心のシンポで知り読んだ。大変勉強になる論文だった。

Fisher は p 値を，統計家がデータの解析結果を「報告」するときのモノサシと位置づけ，比較試験の結果，効果があったか否かの「判定」は，臨床試験の主査である医師が単独あるいはグループ討議によって，報告された p 値，対象とする疾患，症例数等を吟味して総合的に「判定」すべきであると考えた. （p.154）

Neyman-Pearson 検 定では p 値の大きさは問わない.例えば，有意水準を5% に定めるとき，p 􏰀0.0001 であろうがp = 0.049 であろうが，その違いは無視して一律に「有意水準 5% で有意な差あり」とする.(p.155)

Fisher は，科学的知識を深める研究はいくつもの段階からなっており，統計的検定は，その中の一つに適用される方法にすぎない.統計的検定で臨床研究の成果を「判定」するなどとんでもないと考えていたようである.（p.159）

本来Neyman-Pearson流に行けば、「医学的に意味のある差 δ」を設定し、有意水準と検出力からサンプルサイズを設定した上でデータを検定にかけるのだが、これらのステップを無視していきなり検定にかける習慣がこの論文で批判の対象となっている。

私は一応心理学を勉強しているので自分の文脈で考えてみる。

サンプルサイズの設計については村井・橋本（2017）『サンプルサイズ設計入門』であったり、南風原（2014）『続・心理統計学の基礎』であったりに載っているが、基本的なテキストで詳しく扱われることは多くない印象を持っている。

もっとも「心理学的に意味のある差」というのがそもそもどういったものか。これを設定しないことにはNeyman-Pearson流の検定は使えない。だけどこれを設定することの難しさみたいなものが、この手順をすっとばしてくることに繋がったのかもしれない。「心理学的に意味のある差」というのは対象とする心理学的現象によって異なるのだろうし、そもそも意味のある差を「判定」する必要性というのがどれだけあるのかも考えないといけないだろう。

こうした基本的な部分をすっ飛ばして方法論だけを輸入して誤用を続けてきたのが、心理学の歴史な訳である。大切なのは、心理学の具体的な各領域において、統計的な手法に何を任せるべきなのか（意思決定なのか推定なのか等）といった基礎的な議論を改めてすることなのではないかと思った。

心理学のためのサンプルサイズ設計入門 (KS専門書)

心理学のためのサンプルサイズ設計入門 (KS専門書)

続・心理統計学の基礎--統合的理解を広げ深める (有斐閣アルマ)

続・心理統計学の基礎--統合的理解を広げ深める (有斐閣アルマ)

【関連ある過去記事】 nekomosyakushimo.hatenablog.com

心理学における測定について

読んだ本

心理学方法論 (朝倉心理学講座)

心理学方法論 (朝倉心理学講座)

３章「測定をめぐる諸問題」を読んだ。気になったところのメモ。

実験でも理論的も基礎でも臨床でもない領域, それは教育心理学, 発達心理学, 社会心理学といったものであり, 実験心理学よりも具体的な生活文脈に即して対象にアプローチし, 臨床心理学よりも実証を重んじる領域であるといえよう.(p.72)

心理学の各分野の実証を重んじる姿勢の違いについて。

通常, 質問紙調査の場合,「心が狭い」と回答した人に対して, この人は心が広い, とは考えない. 回答者自身の回答を尊重し, この人は心が狭い人だと理解する. このように考える前提には, 回答者は①自身のふだんの行動や心の動きを内省することができ, ②その結果に基づき正直に回答するはずだ, ということがおそらくあるはずである。（p.74）

質問紙調査持つ前提を検討しているが, 改めて言葉にするとすごい前提の上に調査法に思う。

「個性ある機械」としての回答者観, ひいては人間観（p.76）

質問紙調査の前提とする人間観について。

もし, この前提[ある人のある特性には真の値という唯一の値がある（一意に決まる）]を疑うなら, 同一特性・異方法が前提とした「同一」の特性がないかもしれない, ということになる. (中略)そして, 心理的属性・特性が時や状況を通じて基本的に変動しないという前提がないと, （少なくとも古典的テスト理論の）信頼性も妥当性も成立しないのである（p.85）

人には一定程度の多面性, 多様性があり, 誰と接しているときか, あるいは, 何歳頃かによっていくつもの本当の自分がいる, という発想に基づいた測定（論）もありうるのではないかということである.（p.86）

心理学が測定している心理的属性・特性観の問い直し。